Moser’s Circle Problem
For this week we will be discussing a problem that showcases the danger of “patterns” in math and why rigorous proofs are necessary to make any meaningful claim. The problem we will be exploring is known as Moser’s Circle Problem which starts off with a simple pattern that eventually breaks and calls for a more complicated method of proof.
The Problem
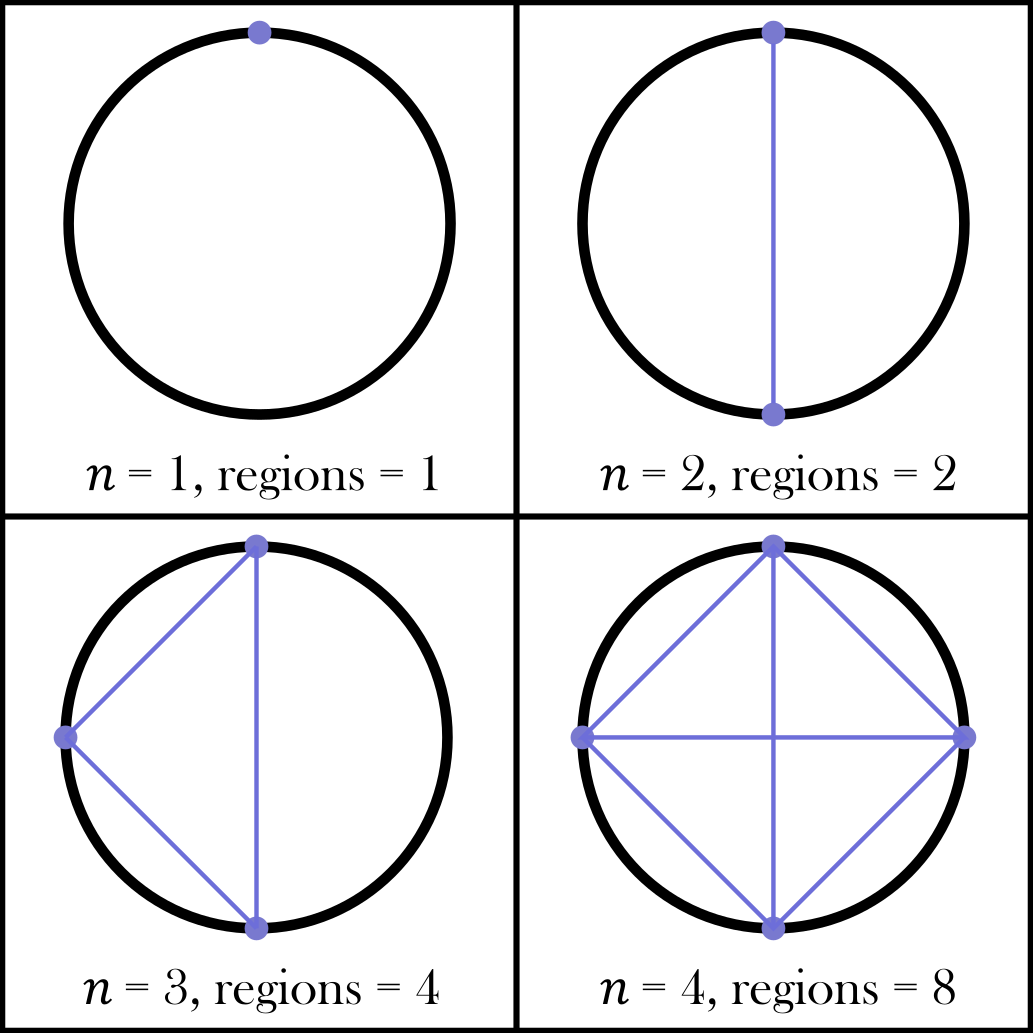
This problem is concerned with the number of regions that will form after 𝒏 points are chosen on the circumference of a circle and a line is drawn passing through any 2 points. We can try to solve the problem by considering a few base cases of n = 1, 2, 3, 4 and then trying to form an equation based on this.
Based on the information we have we can see that we have a sequence 1, 2, 4, 8, … which resembles the powers of 2 starting at 1. Thus, we can model this sequence using the formula 2ⁿ⁻¹.
To test our hypothesis we can see if this formula works for the next two cases, 𝒏 = 5, 6.
As we can see our pattern of powers of 2 fails at 𝒏 = 6 which means that we will have to take a different approach to find a general solution to this problem.
The Solution
This approach requires a general understanding of combinatorics so if you do not know about combinations and permutations I would recommend reading the excerpt on this website in order to fully understand this solution.
First, we consider the number of lines that can be formed. Since two points determine a line the number of lines that can be formed is given by the formula:
This is because we can choose any two of the 𝒏 points and form a line with them.
Next, we can consider the number of intersections that are formed when two lines intersect. This can be done in a similar way by considering the fact two lines intersect when we choose any 4 points to form 2 lines out of the total 𝒏 points.
Finally to count the number of regions formed we can consider the fact that the number of regions formed is equal to the number of lines + the number of intersections. This is because a new region is formed when two points form a line and that line crosses a previously existing region.
Consider the first picture in this article where we have 𝒏 = 2. We can clearly see that the two points form a line and then this line cuts the previous region (the whole circle) into two regions and thus we have added 1 new region, so far there are no intersections so this can be counted as 0. We can also see the same concept with 𝒏 = 3 where we create 2 new lines and they both intersect one region (half of the circle) to form two new regions.
When no intersections occur between lines, the number of new regions formed is equal to the number of lines since the lines only intersect regions of the circle and not other lines. However, if the line intersects another line then it divides the regions formed by that line (and other lines) into more regions and thus the number of regions is equal to:
We can illustrate this with an example:
As you can see the new line intersects the regions created by the other line as well as the line itself! This creates two new regions or 1 more than the number of intersections, but why?
The reason for this is that for 𝒏 = 0, there is 1 region already existing (the circle itself. Thus our final equation becomes:
This is a valid way to write the equation, however, it can also be written as a polynomial with the form:
This problem showcases why it is so crucial that we prove every step in mathematics. When our method for solving this problem involved purely observations, we made mistakes with our analysis, but once we began to prove each of our steps we arrived at the correct answer. That is why it is important in mathematics to make observations that give you a general direction, but not to rely solely on these observations when it comes to solving problems.







I don’t entirely get the reason for the +1 in the regions equation